递归树
递归树与时间复杂度分析
递归的思想就是,将大问题分解为小问题来求解,然后再将小问题分解为小小问题。这样一层一层地分解,直到问题的数据规模被分解得足够小,不用继续递归分解为止。
如果我们把这个一层一层的分解过程画成图,它其实就是一棵树。我们给这棵树起一个名字,叫作递归树。我这里画了一棵斐波那契数列的递归树,你可以看看。节点里的数字表示数据的规模,一个节点的求解可以分解为左右子节点两个问题的求解。
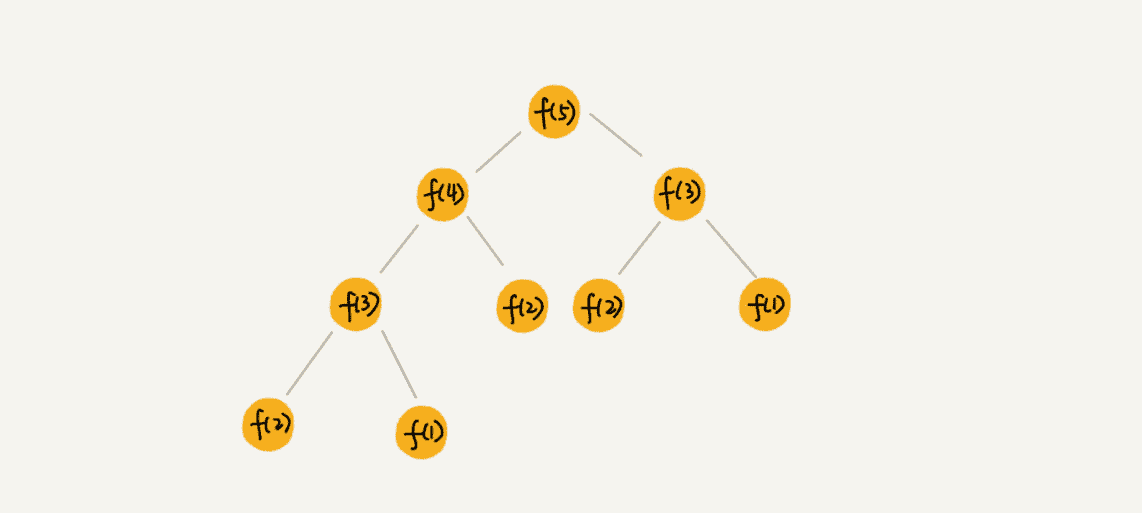
现在,我们就来看,如何用递归树来求解时间复杂度。
归并排序每次会将数据规模一分为二。我们把归并排序画成递归树,就是下面这个样子:
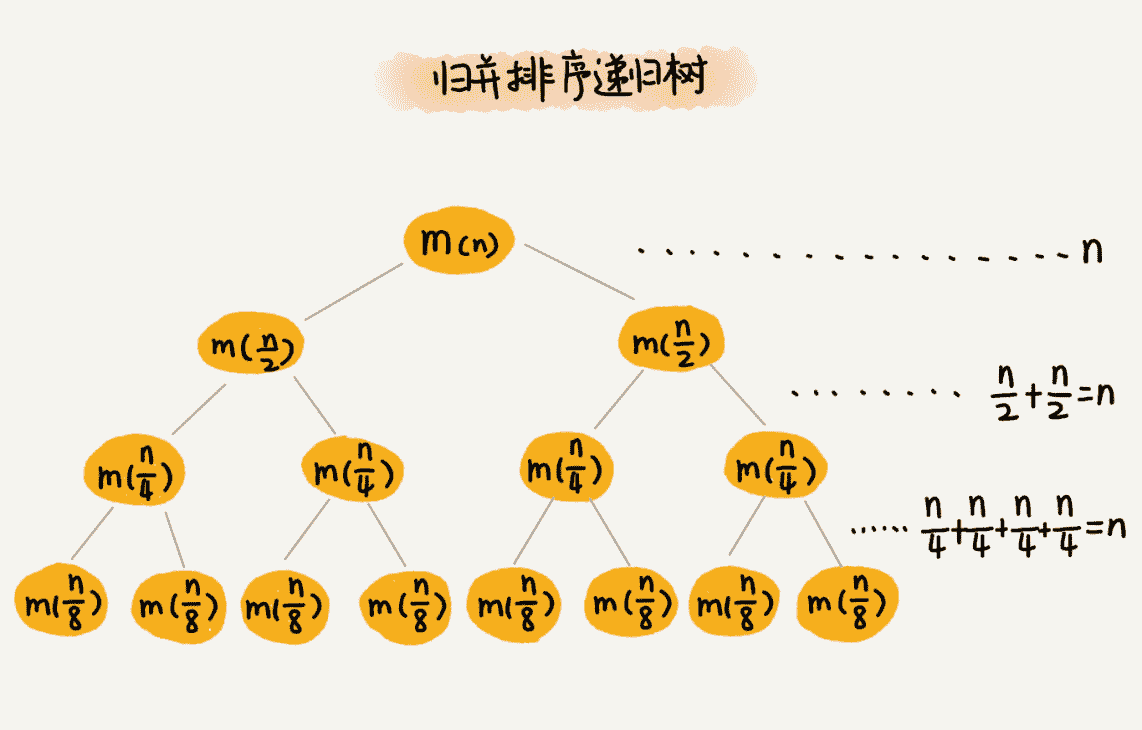
因为每次分解都是一分为二,所以代价很低,我们把时间上的消耗记作常量 1 。归并算法中比较耗时的是归并操作,也就是把两个子数组合并为大数组。从图中我们可以看出,每一层归并操作消耗的时间总和是一样的,跟要排序的数据规模有关。我们把每一层归并操作消耗的时间记作$n$。
现在,我们只需要知道这棵树的高度$h$,用高度$h$乘以每一层的时间消耗$n$,就可以得到总的时间复杂度$O(n*h)$。
从归并排序的原理和递归树,可以看出来,归并排序递归树是一棵满二叉树。满二叉树的高度大约是$\log_{2}n$,所以,归并排序递归实现的时间复杂度就是$O(n\log n)$。我这里的时间复杂度都是估算的,对树的高度的计算也没有那么精确,但是这并不影响复杂度的计算结果。
分析快速排序的时间复杂度
快速排序在最好情况下,每次分区都能一分为二,这个时候用递推公式$T(n)=2T(\frac{n}{2})+n$,很容易就能推导出时间复杂度是$O(n\log n)$。但是,我们并不可能每次分区都这么幸运,正好一分为二。
我们假设平均情况下,每次分区之后,两个分区的大小比例为$1:k$。当$k=9$时,如果用递推公式的方法来求解时间复杂度的话,递推公式就写成$T(n)=T(\frac{n}{10})+T(\frac{9n}{10})+n$。
这个公式可以推导出时间复杂度,但是推导过程非常复杂。那我们来看看,用递归树来分析快速排序的平均情况时间复杂度,是不是比较简单呢?
我们还是取$k$等于$9$,也就是说,每次分区都很不平均,一个分区是另一个分区的$9$倍。如果我们把递归分解的过程画成递归树,就是下面这个样子:
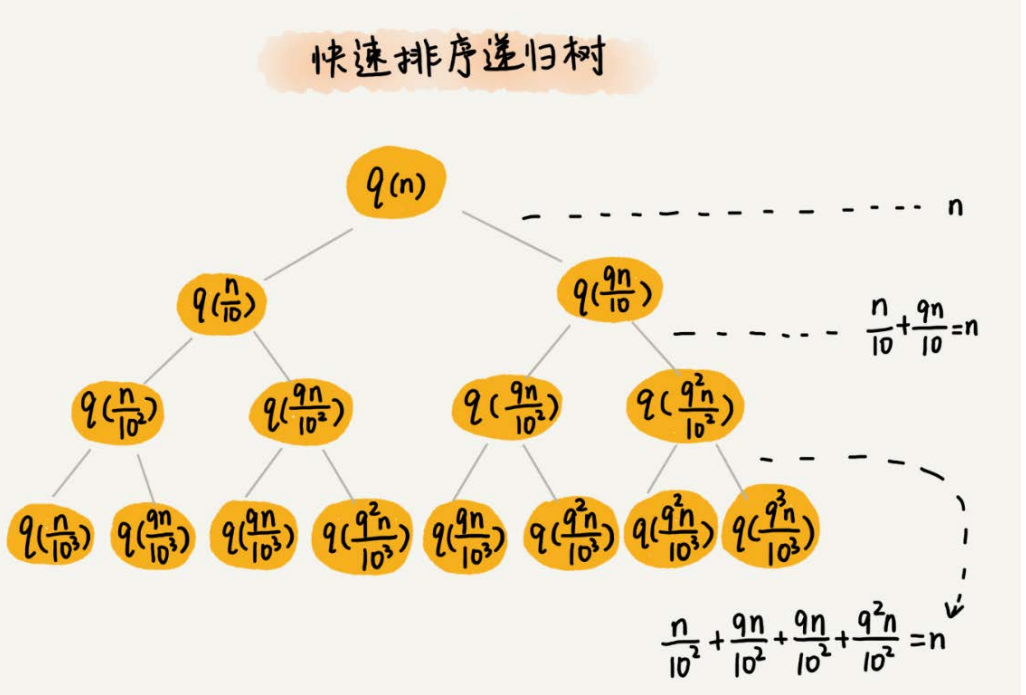
快速排序的过程中,每次分区都要遍历待分区区间的所有数据,所以,每一层分区操作所遍历的数据的个数之和就是$n$。我们现在只要求出递归树的高度$h$,这个快排过程遍历的数据个数就是 $h * n$ ,也就是说,时间复杂度就是$O(h * n)$。
因为每次分区并不是均匀地一分为二,所以递归树并不是满二叉树。这样一个递归树的高度是多少呢?
我们知道,快速排序结束的条件就是待排序的小区间,大小为$1$,也就是说叶子节点里的数据规模是$1$。从根节点$n$到叶子节点$1$,递归树中最短的一个路径每次都乘以$\frac{1}{10}$,最长的一个路径每次都乘以$\frac{9}{10}$。通过计算,我们可以得到,从根节点到叶子节点的最短路径是$\log_{10}n$,最长的路径是$\log_{\frac{10}{9}}n$。
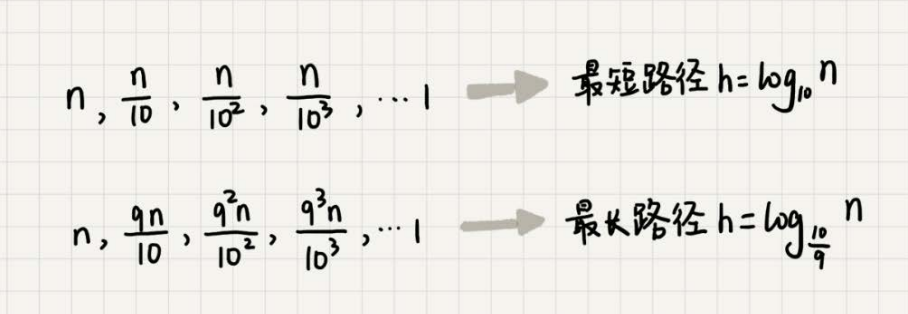
所以,遍历数据的个数总和就介于$n\log_{10}n$和$n\log_{\frac{10}{9}}n$之间。根据复杂度的大O表示法,对数复杂度的底数不管是多少,我们统一写成$\log n$,所以,当分区大小比例是$1:9$时,快速排序的时间复杂度仍然是$O(n\log n)$。
刚刚我们假设$k=9$,那如果$k=99$,也就是说,每次分区极其不平均,两个区间大小是$1:99$,这个时候的时间复杂度是多少呢?
我们可以类比上面$k=9$的分析过程。当$k=99$的时候,树的最短路径就是$\log_{100}n$,最长路径是$\log_{\frac{100}{99}}n$,所以总遍历数据个数介于$n\log_{100}n$和$n\log_{\frac{100}{99}}n$之间。尽管底数变了,但是时间复杂度也仍然是$O(n\log n)$。
也就是说,对于$k$等于$9$,$99$,甚至是$999$,$9999$……,只要$k$的值不随$n$变化,是一个事先确定的常量,那快排的时间复杂度就是$O(n\log n)$。所以,从概率论的角度来说,快排的平均时间复杂度就是$O(n\log n)$。
分析斐波那契数列的时间复杂度
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return f(n-1) + f(n-2);
}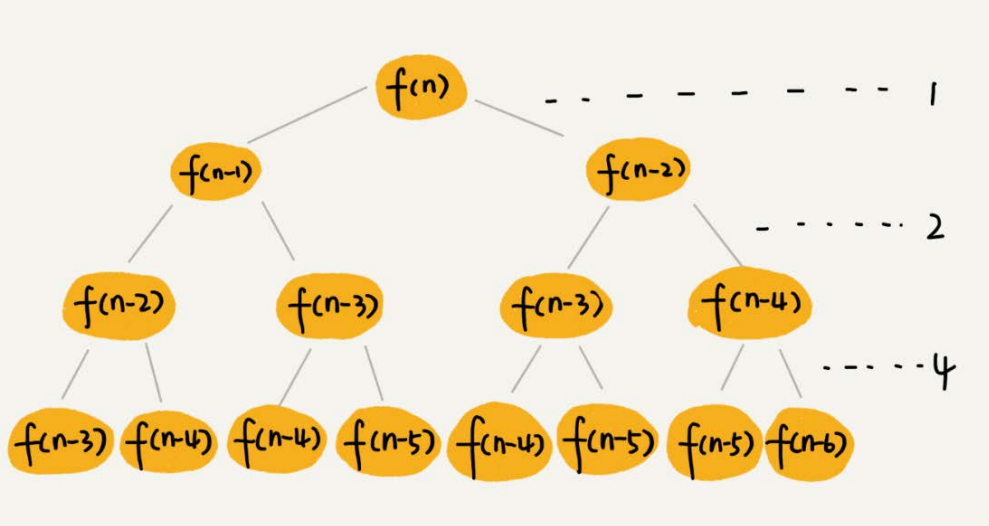
$f(n)$分解为$f(n-1)$和$f(n-2)$,每次数据规模都是$-1$或者$-2$,叶子节点的数据规模是$1$或者$2$。所以,从根节点走到叶子节点,每条路径是长短不一的。如果每次都是$-1$,那最长路径大约就是$n$;如果每次都是$-2$,那最短路径大约就是$\frac{n}{2}$。
每次分解之后的合并操作只需要一次加法运算,我们把这次加法运算的时间消耗记作$1$。所以,从上往下,第一层的总时间消耗是$1$,第二层的总时间消耗是$2$,第三层的总时间消耗就是$2^{2}$。依次类推,第$k$层的时间消耗就是$2^{k-1}$,那整个算法的总的时间消耗就是每一层时间消耗之和。
如果路径长度都为$n$,那这个总和就是$2^{n}-1$。
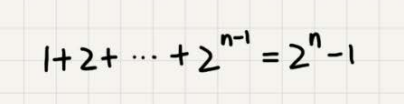
如果路径长度都是$\frac{n}{2}$ ,那整个算法的总的时间消耗就是$2^{\frac{n}{2}}-1$
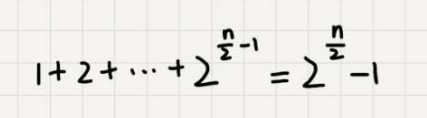
所以,这个算法的时间复杂度就介于$O(2^{n})$和$O(2^{\frac{n}{2}})$之间。虽然这样得到的结果还不够精确,只是一个范围,但是我们也基本上知道了上面算法的时间复杂度是指数级的,非常高。
分析全排列的时间复杂度
全排列问题:如何把$n$个数据的所有排列都找出来
比如,$1, 2,3$这样$3$个数据,有下面这几种不同的排列:
1,2,3 | 1,3,2 | 2,1,3 | 2,3,1 | 3,1,2 | 3,2,1
如何编程打印一组数据的所有排列呢?这里就可以用递归来实现。
如果我们确定了最后一位数据,那就变成了求解剩下$n-1$个数据的排列问题。而最后一位数据可以是$n$个数据中的任意一个,因此它的取值就有$n$种情况。所以,“$n$个数据的排列”问题,就可以分解成$n$个“$n-1$个数据的排列”的子问题。
假设数组中存储的是1,2, 3…n
f(1,2,…n) = {最后一位是1, f(n-1)} + {最后一位是2, f(n-1)} +…+{最后一位是n, f(n-1)}
如果我们把递推公式改写成代码,就是下面这个样子:
// 调用方式:
// int[]a = a={1, 2, 3, 4}; printPermutations(a, 4, 4);
// k表示要处理的子数组的数据个数
public void printPermutations(int[] data, int n, int k) {
if (k == 1) {
for (int i = 0; i < n; ++i) {
System.out.print(data[i] + " ");
}
System.out.println();
}
for (int i = 0; i < k; ++i) {
int tmp = data[i];
data[i] = data[k-1];
data[k-1] = tmp;
printPermutations(data, n, k - 1);
tmp = data[i];
data[i] = data[k-1];
data[k-1] = tmp;
}
}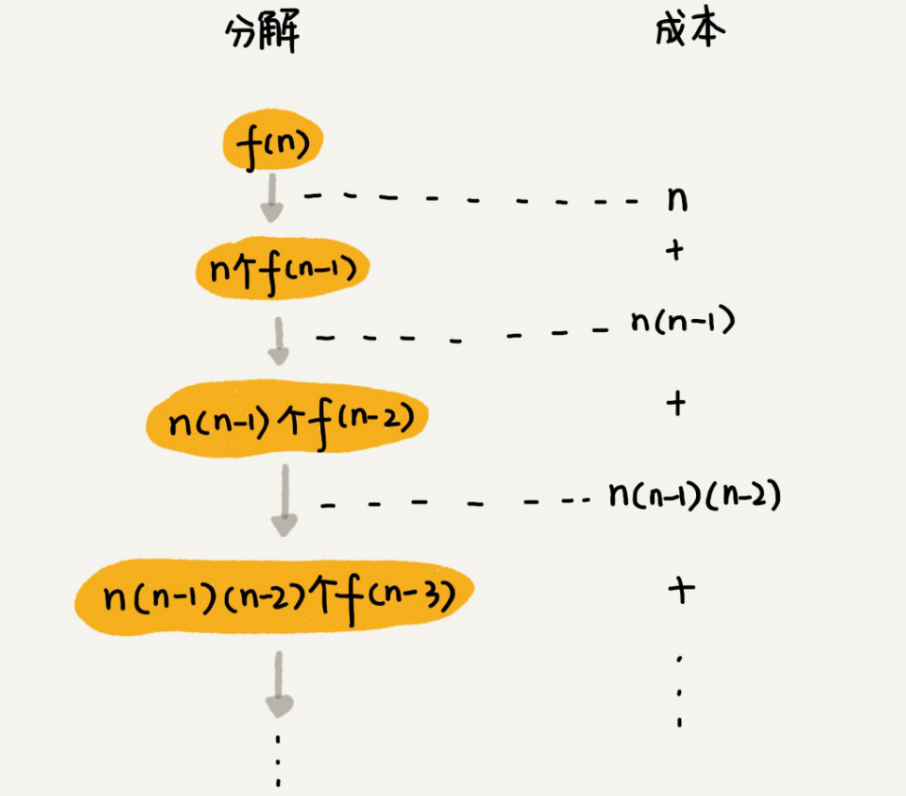
第一层分解有$n$次交换操作,第二层有$n$个节点,每个节点分解需要$n-1$次交换,所以第二层总的交换次数是$n*(n-1)$。第三层有$n*(n-1)$个节点,每个节点分解需要$n-2$次交换,所以第三层总的交换次数是$n*(n-1)*(n-2)$。
以此类推,第$k$层总的交换次数就是$n * (n-1) * (n-2) * … * (n-k+1)$。最后一层的交换次数就是$n * (n-1) * (n-2) * … * 2 * 1$。每一层的交换次数之和就是总的交换次数。
$$n + n*(n-1) + n*(n-1)*(n-2) +... + n*(n-1)*(n-2)*...*2*1$$这个公式的求和比较复杂,我们看最后一个数,$n * (n-1) * (n-2) * … * 2 * 1$等于$n!$,而前面的$n-1$个数都小于最后一个数,所以,总和肯定小于$n * n!$,也就是说,全排列的递归算法的时间复杂度大于$O(n!)$,小于$O(n * n!)$,虽然我们没法知道非常精确的时间复杂度,但是这样一个范围已经让我们知道,全排列的时间复杂度是非常高的。