Merkle Tree

什么是 Merkle Tree

定义

Merkle Tree，也叫默克尔树或哈希树，是区块链的底层加密技术，被比特币和以太坊区块链广泛采用。Merkle Tree是一种自下而上构建的加密树，每个叶子是对应数据的哈希，而每个非叶子为它的2个子节点的哈希。

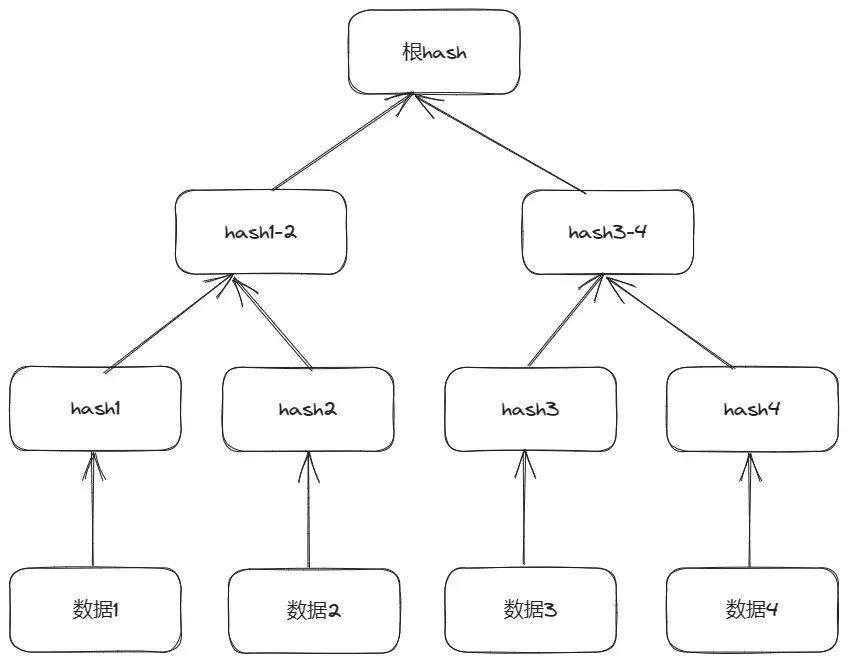
img.png

Merle Tree Root 的计算过程

假定一个区块包括A,B,C,D四个交易，下标分别是0,1,2,3;计算根哈希的方式如图:

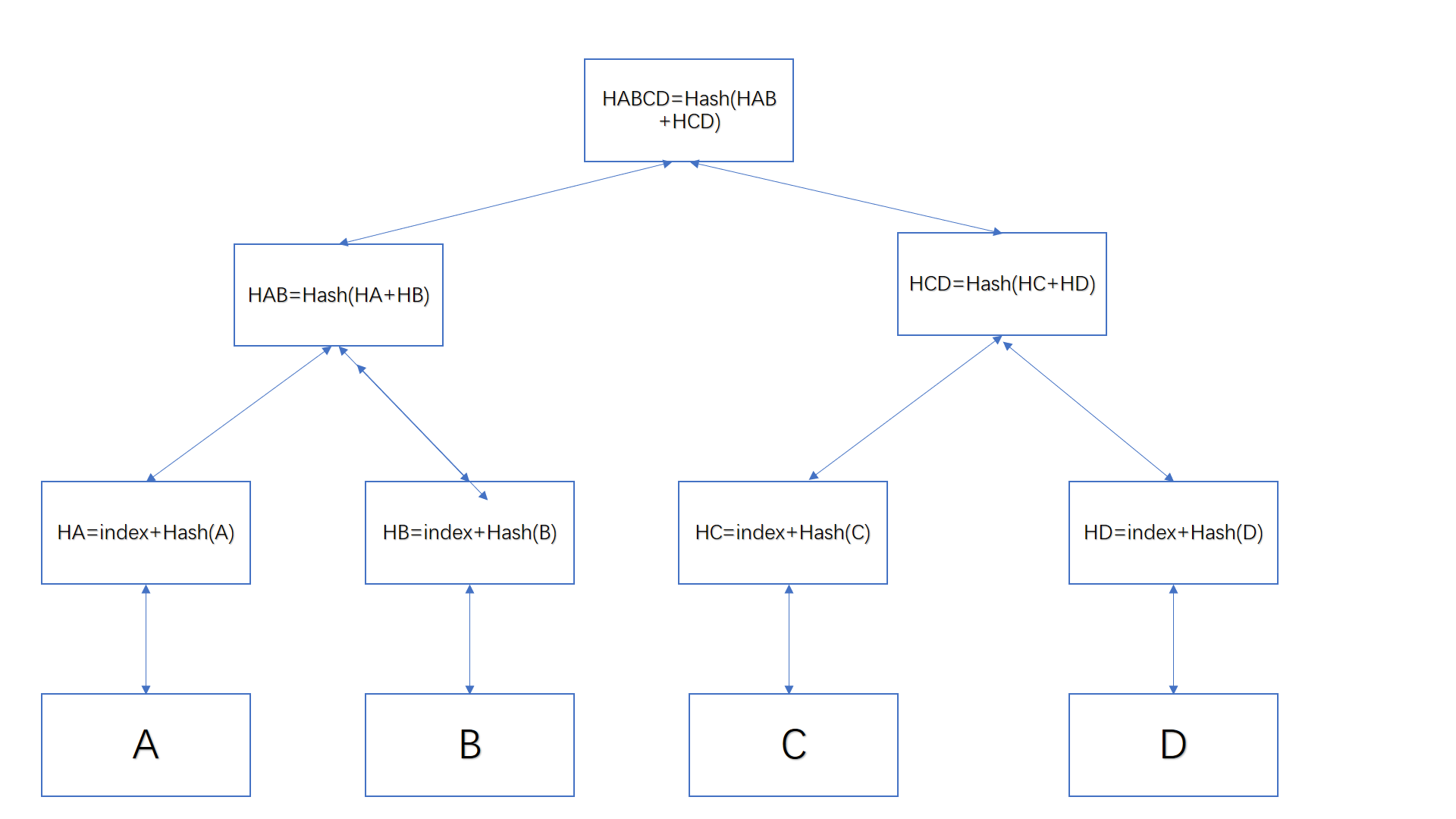
img.png

计算步骤如下： 1，将交易的下标做rlp编码拼接上交易的哈希，作为叶子节点。 2，将节点元素n（上图n为2）个一组，拼接起来计算哈希值，作为上一层元素。 3，重复步骤2，直到当前元素只有一个，计算过程结束。

Merkle证明主要用于跨链交易过程（交易树）中的交易存在性证明，根据跨链交易所涉及的交易/回执去请求各个链的Proof；根据交易/回执，Transaction/Receipt Root，以及Proof完成Merkle证明；如果验证不通过，交易终止，否则执行跨链交易；各个链上各自执行跨链交易，返回交易回执以及proof；验证交易回执，不通过则回滚，否则完成跨链交易。跨链交易借助Merkle证明实现了一种可信消息验证机制，能够有效地验证交易的真实性，为跨链交易的正确执行提供了安全保障。

Merkle 证明：对于HD来说，它的 merkle proof 就是节点 (HABCD，HAB，HC)

Merkle Tree 的应用

证明某个集合中存在或不存在某个元素

通过构建集合的默克尔树，并提供该元素各级兄弟节点中的 Hash 值，可以不暴露集合完整内容而证明某元素存在。

另外，对于可以进行排序的集合，可以将不存在元素的位置用空值代替，以此构建稀疏默克尔树（Sparse Merkle Tree）。该结构可以证明某个集合中不包括指定元素。

稀疏默克尔树

稀疏默克尔树（Sparse Merkle Tree，SMT）与默克尔树基本类似，只是数据是有序的。

例如有一个四个叶子节点的SMT，然后有数据A和D，那么这SMT如下：

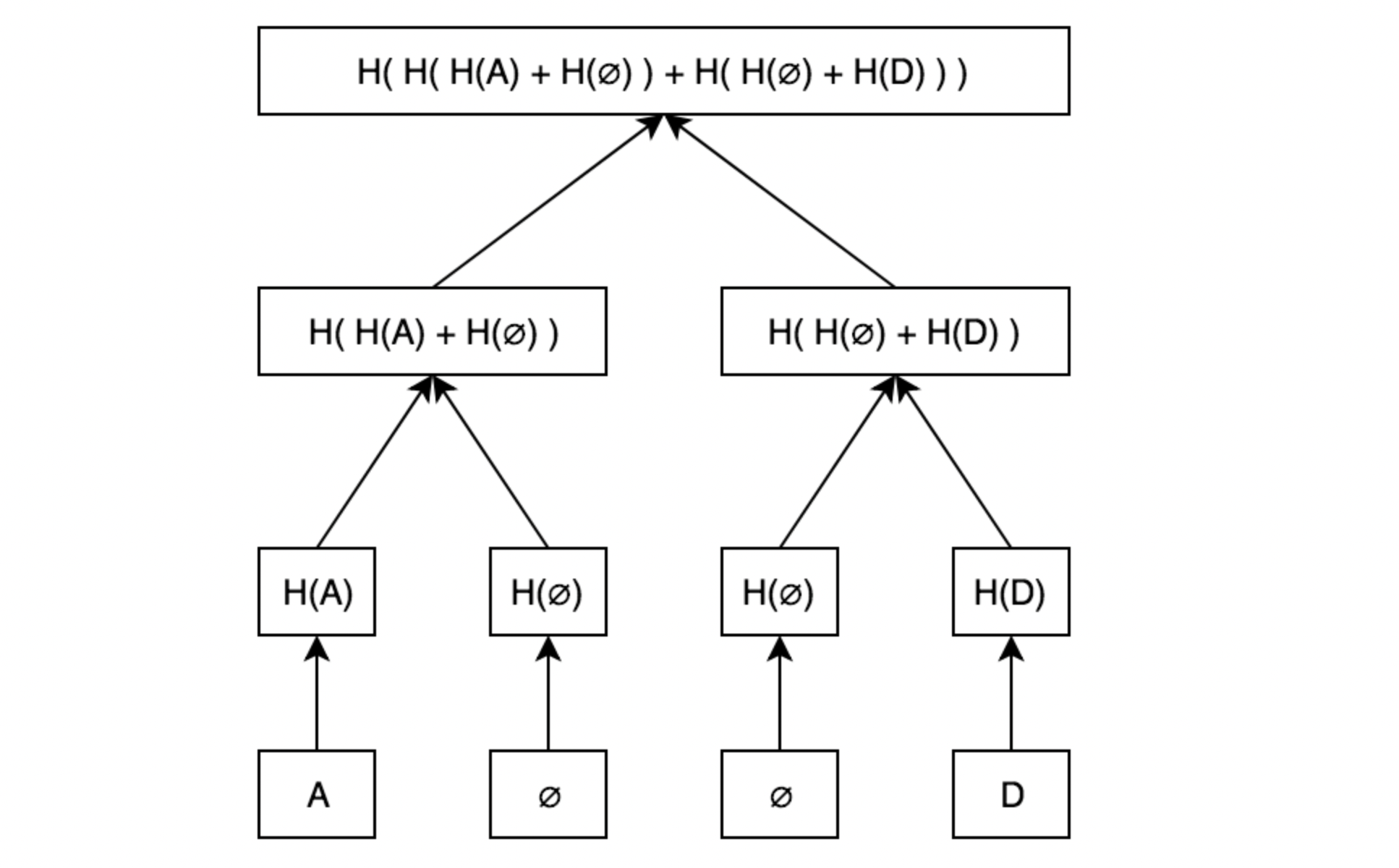
img.png

可以看到，A和D被有序的放到了索引是0和3的位置，而所以是1和2的位置是null。 例如需要证明C不存在，那么只需证明索引3处是null即可，也就转化为常规的默克尔证明，只需给出H(H(A)+H(null))和H(D)，如下图所示：

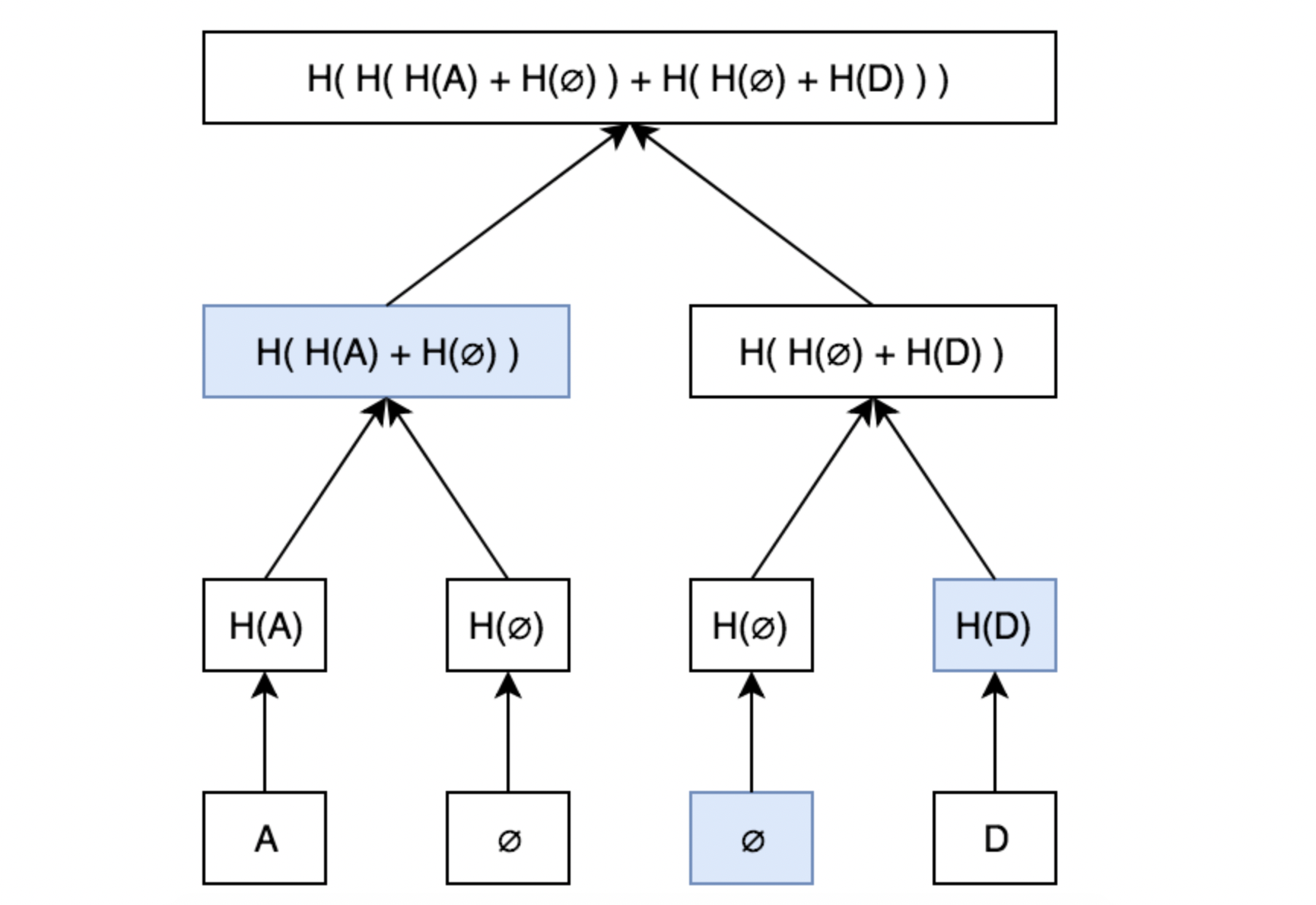
img.png

快速比较大量数据

对每组数据排序后（保证构建有序）构建默克尔树结构。当两个默克尔树根相同时，则意味着所代表的两组数据必然相同。否则，必然不同。

由于 Hash 计算的过程可以十分快速，预处理可以在短时间内完成。利用默克尔树结构能带来巨大的比较性能优势。

快速定位修改

以下图为例，基于数据 D0……D3 构造默克尔树，如果 D1 中数据被修改，会影响到 N1，N4 和 Root。

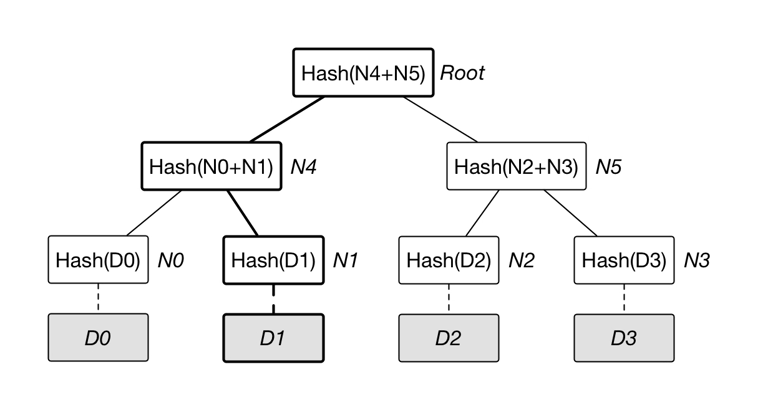
img.png

因此，一旦发现某个节点如 Root 的数值发生变化，沿着 Root –> N4 –> N1，最多通过 O(lgN) 时间即可快速定位到实际发生改变的数据块 D1。

零知识证明

仍以上图为例，如何向他人证明拥有某个数据 D0 而不暴露其它信息。挑战者提供随机数据 D1，D2 和 D3，或由证明人生成（需要加入特定信息避免被人复用证明过程）。

证明人构造如图所示的默克尔树，公布 N1，N5，Root。验证者自行计算 Root 值，验证是否跟提供值一致，即可很容易检测 D0 存在。整个过程中验证者无法获知与 D0 相关的额外信息。